Moment of inertia is the product of first moment of area and the centroidal distance of the area from a given axis. If A.x is the first moment of area of certain section then (Ax).x is the moment of inertia (second moment of area)of that section.
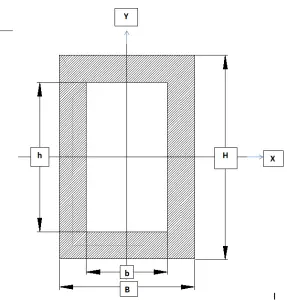
moment of inertia of hollow section can be found by first calculating the inertia of larger rectangle and then by subtracting the hollow portion from that large rectangle.
Moment of Inertia About X-axis
\( I_{x}=\frac{BH^{3}}{12}- \frac{bh^{3}}{12}\)Moment of Inertia About Y-axis
\( I_{y}= \frac{HB^{3}}{12}- \frac{hb^{3}}{12} \)Example
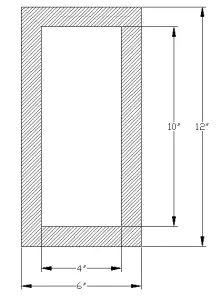
Find moment of inertia of a hollow rectangular section given below.
solution
Moment of Inertia About X-axis
\( I_{x}= \frac{BH^{3}}{12}- \frac{bh^{3}}{12}\)..
\( I_{x}= \frac{6\times 12^{3}}{12}-\frac{4\times 10^{3}}{12}\)\( I_{x}=530.67\space in^{4}\)