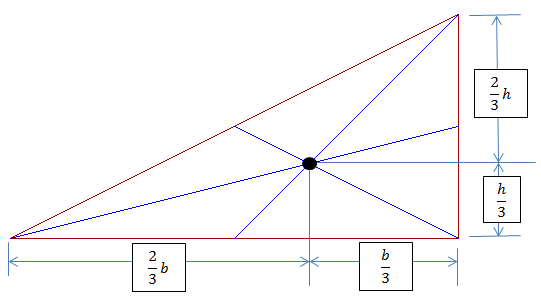
Center of gravity (centroid) of a triangle lies at a common point where the medians of geometric figures intersect each other. For determining centroid draw a lines from medians of each face to the corner of opposite sides. As shown in the figure below:
Centroid of Triangle
Example
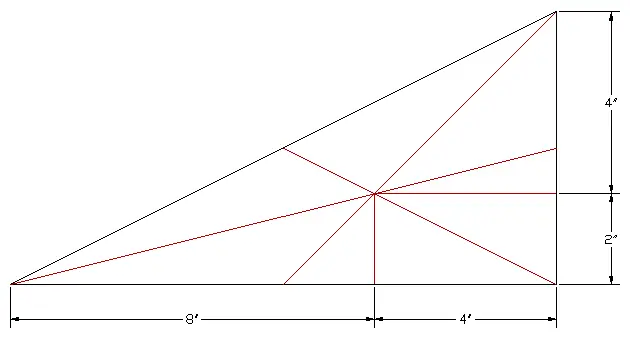
Find the centroid of triangle having b= 12’ and h= 6’.
Solution:
Centroid of triangle is a point where medians of geometric figures intersect each other. In case of triangle this point is located at 2b/3 horizontally from reference y-axis or from extreme left vertical line. And h/3 vertically from reference x-axis or from extreme bottom horizontal line line.
Hence, from extreme left line = 2b/3 = (2×12)/3 = 8′
similarly, h/3 vertically from extreme bottom horizontal line = 6/3 = 2′
Now draw a vertical line at a distance of 2b/3 from reference x-axis. In the same way draw a horizontal line at a distance of h/3. A point where two lines will intersect will the centroid of triangle.
As shown in the figure below:
Centroid of Triangle Solution
